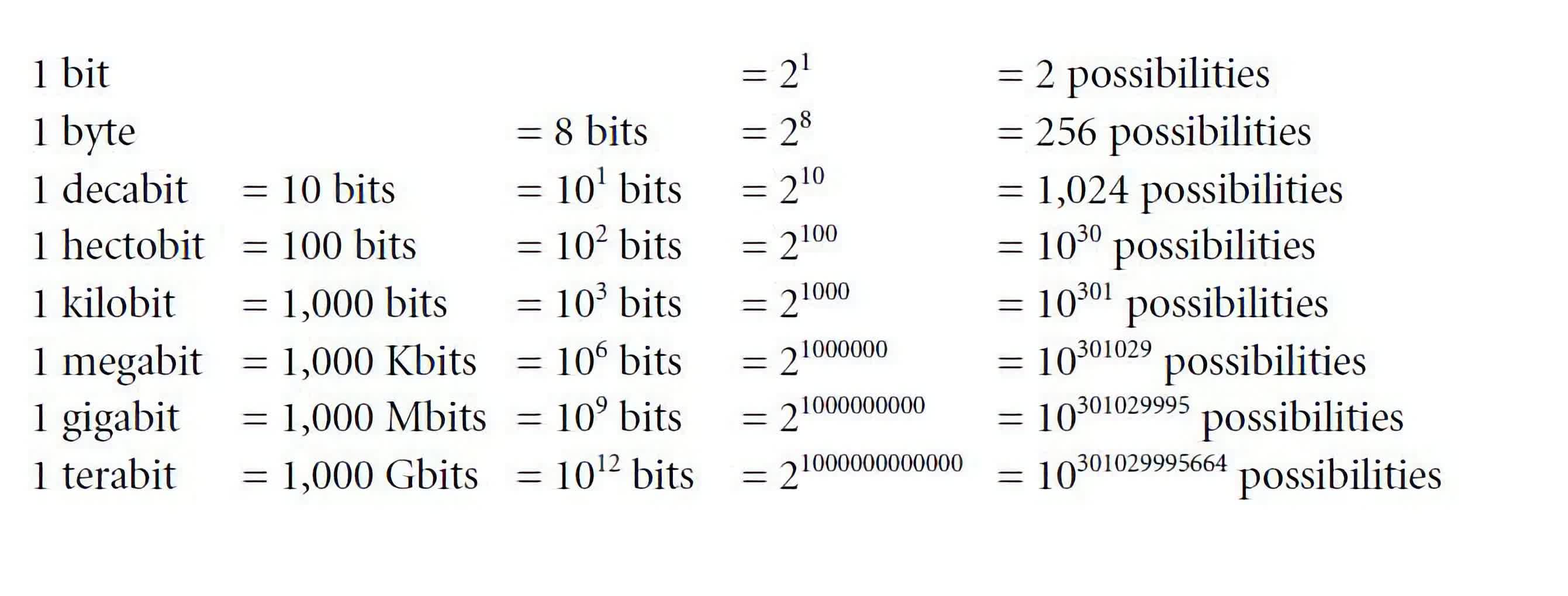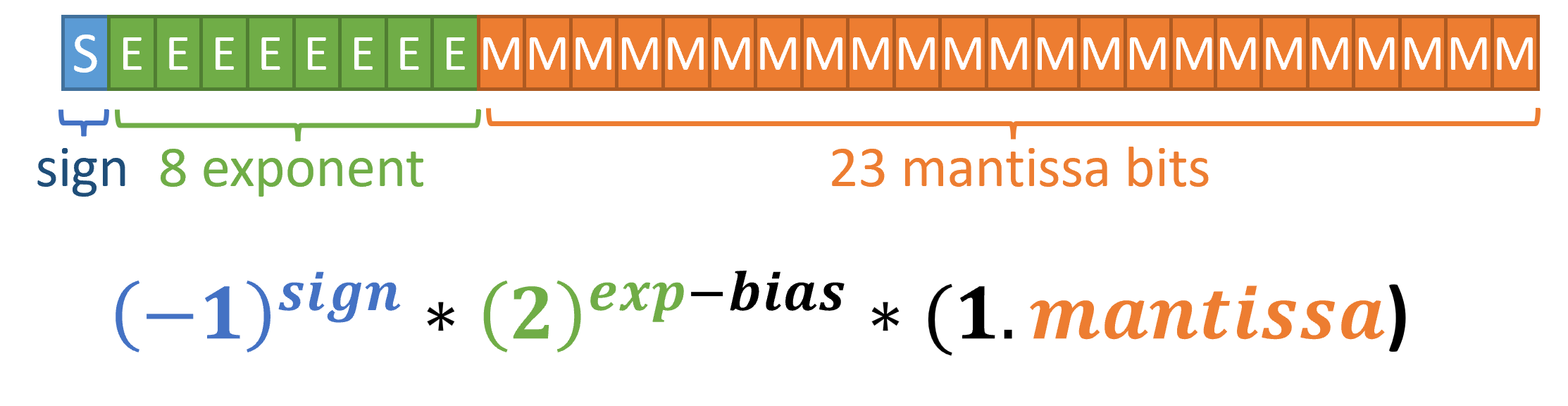As Shakespeare would have it, “that which we name a rose by every other identify would scent simply as candy.” However on this planet of computer systems, that method by which we symbolize a quantity in {hardware} can imply the distinction between a blazing quick machine or a expensive $475 million bug — Pentium 4 anybody?
Welcome to arguably probably the most basic element of laptop design: how numbers are represented in {hardware}! Everyone knows that trendy computer systems function on binary numbers and are extraordinarily environment friendly at doing so. However this was not at all times the case. And what’s extra, many tech giants as we speak, together with Microsoft, Nvidia, Intel, Arm, and Tesla are all revisiting how they encode numbers in {hardware}, as a way to squeeze out each final little bit of efficiency.
However we’re getting somewhat forward of ourselves. On this article, we’ll check out how this all got here to be. From the early inception of binary numbers to the fashionable world of floating level, this seemingly easy idea can change into fairly complicated, so let’s begin from the start…
From Pure Numbers to Binary Numbers
Once we first find out about numbers in grade faculty, we sometimes start with pure numbers (1, 2, 3, 4…). Pure numbers are utilized in all kinds of day-to-day conditions, from counting objects to financial transactions, and a mess of how in-between. Finally, we be taught concerning the idea of zero, and over time get launched to extra superior ideas comparable to detrimental numbers, complicated numbers, and algebraic variables.
The power to carry out computations on numbers expands their utility past simply counting issues. Easy transaction-based computations use addition and subtraction; multiplication and division could be leveraged to hurry up the fundamental computational arithmetic; and ultimately complicated equations and algorithms may also help remedy unknowns.
Primary numbers and arithmetic is perhaps simple for a human to wrap their thoughts round, however how would a machine do all of this, and, probably, do it even sooner than a human? Effectively, this was exactly the query Gottried Lebniz would spend his life attempting to reply, again within the 1600s.
A Historic Walkthrough: The Invention of Binary
Leibniz (1646-1716) was a German polymath, energetic in regulation, philosophy, arithmetic, languages, science, and theology. Within the arithmetic area, he’s most well-known for his impartial invention of calculus alongside Isaac Newton. His invention of binary arithmetics and hexadecimal notation would go unnoticed for hundreds of years, till it will definitely led to the inspiration of as we speak’s world of digital computing and communication.
When he wasn’t inventing calculus or consumed together with his many mental endeavors, Leibniz was consumed with discovering a technique to carry out computations rapidly. He didn’t wish to “waste” time performing “easy” operations comparable to addition and subtraction, and was satisfied that there should be a technique to distill info into a really fundamental type for fast math.
A deeply spiritual man dwelling within the Holy Roman Empire, Leibniz believed that numbers and math have been divinely impressed, and was set on discovering a technique to join the 2. He first developed a quantity system in 1679 in a manuscript known as, “On the Binary Development” to symbolize numbers utilizing simply 0s and 1s. Whereas he was in a position to symbolize numbers in a “easy” method utilizing binary notation, he discovered binary calculations to be “longer, albeit simpler.” Quick-forward to the twentieth century, and this could really change into the elemental tenant for binary computer systems.
Binary Primer
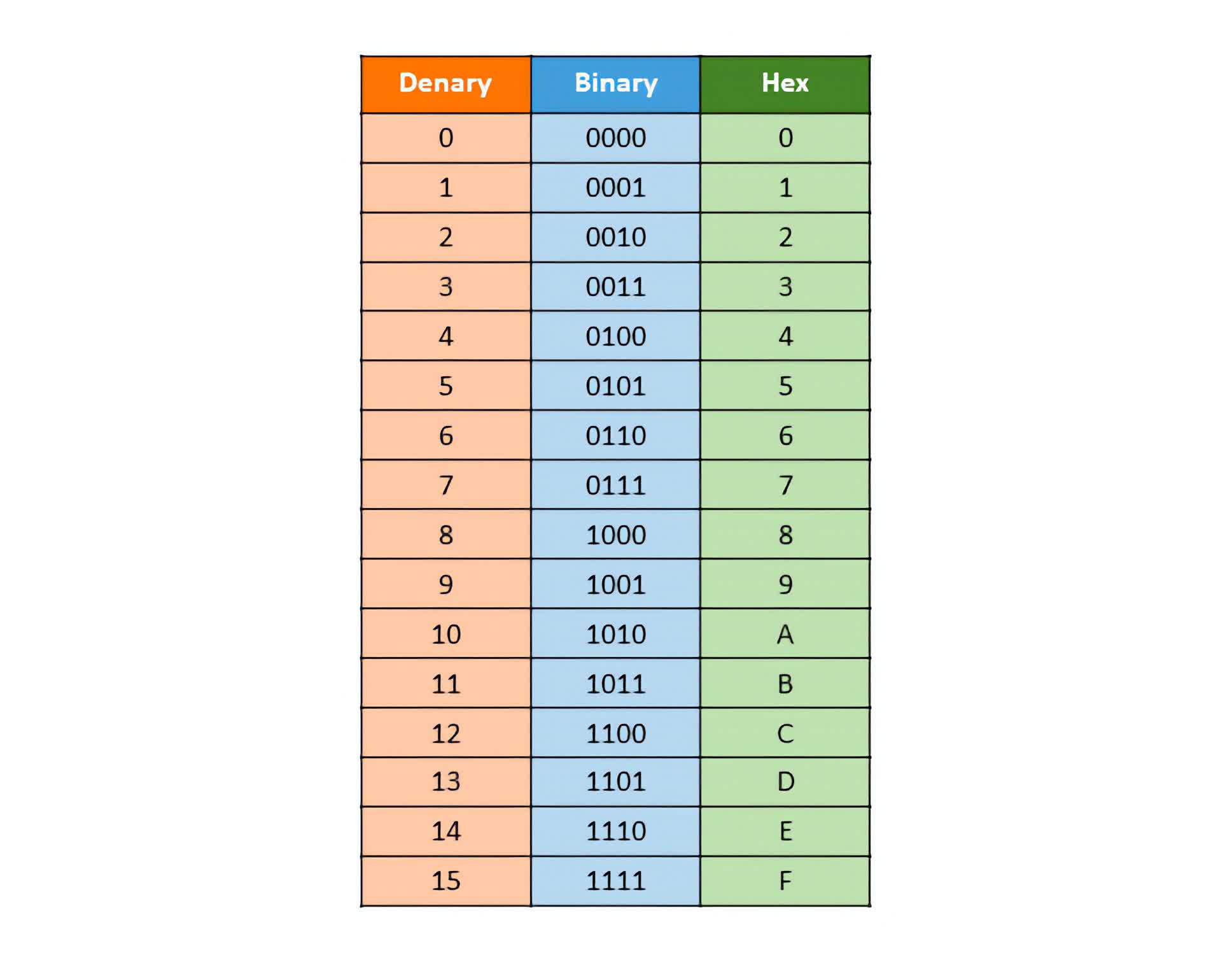
Technically talking, Leibniz got here up with a technique to symbolize any decimal quantity (that’s, a base 10 quantity, which people sometimes use) as a binary quantity (base 2), the place every bit represents an influence of two.
For instance, the decimal quantity 5 could be represented in binary as 101, with the rightmost bit representing 2^0 (= 1), the center bit representing 2^1 (= 2), and the leftmost bit representing 2^2 (= 4).
| Decimal | Binary |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
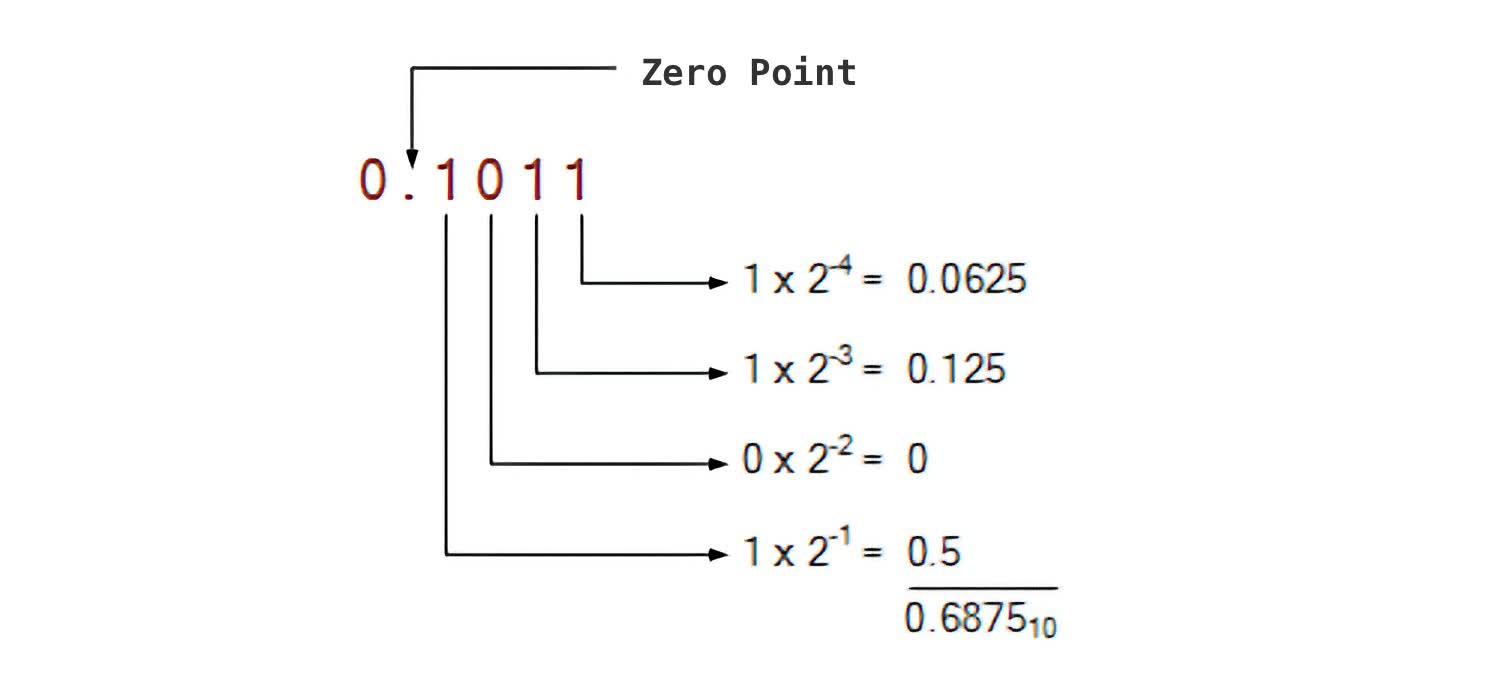
Utilizing this formulation, you may symbolize any decimal quantity, because the desk above exhibits. Moreover, you may introduce a binary level (cannot simply name them decimal factors now, can we?) and symbolize fractions. Mathematically, this could be akin to elevating to detrimental exponent values. The decimal quantity 0.6875 could be represented in binary as 0.1011, with the rightmost bit within the case representing 2^-4 (= 0.0625).
Leibniz revisited binary numbers about 20 years later, in 1697, throughout a dialogue with Duke Rudolph of Brunswick and Luneburg, who made the connection between binary numbers and the idea of creation ex nihilo, in keeping with which all issues have been created from nothing by the one God. Excited by the revelation (along with much more “proof” of divine illustration of numbers from Christian missionaries in China studying about Yin and Yang’s binary nature), Leibniz was consumed the remainder of his life working to persuade the general public about his discovery.
Though his theological connection by no means took maintain with public opinion, he did launch many manuscripts on fascinating phenomena when utilizing binary to symbolize pure numbers.
For instance, Leibniz famous an fascinating property of geometric development (e.g., 1, 2, 4, 8, 16, 32, …) that was on the coronary heart of binary numeration, particularly, that the sum of any three consecutive phrases is always divisible by 7. This, together with a mess of “random” discoveries that Leibniz got here throughout, helped persuade him concerning the significance of binary illustration, but it surely by no means really took off as a technique to do actual math till the twentieth century and the digital revolution stumbled upon it.
From Binary to Hexadecimal Numbers
Throughout these years, Leibniz additionally considered different quantity codecs comparable to base 12 and 16, in an effort to deal with the “longer, albeit simpler” nature of binary, mathematically. His discovery of hexadecimal was the primary to introduce the letters a, b, c, d, e, and f to symbolize 10, 11, 12, 13, 14, and 15, which we as we speak see in lots of functions.
As a fast primer, our “pure” method of utilizing numbers in on a regular basis interactions makes use of base 10. This primarily implies that we’ve got 10 symbols (0, 1, 2, …, 8, and 9), and as soon as we run out of symbols, we reuse the symbols within the subsequent “place” to maintain counting. With this technique, we will encode any arbitrary worth utilizing our set of predetermined symbols.
Within the binary system, there exists solely two symbols: 0 and 1. In any other case, the methodology holds the identical to the decimal system: 0 is encoded as 0, 1 is encoded as 1, after which 2 is encoded as 10 (since we “ran out” of symbols). As Leibniz stated, that is technically quite simple, however will end in extra “digits” for numbers. However, looking forward to the invention of the transistor within the twentieth century, the binary system naturally lends itself to the on/off nature of a change.
Whereas the conversion of numbers between decimal and binary is not too complicated, performing computations in binary (for a human) can get a bit unwieldy and is error-prone, given the numerous digits of the encoding format. A whole area intersecting between math and laptop science was created to raised grasp the character of computing with zeros and ones.
Boolean Algebra and Data Concept
Whereas Leibniz may need launched the notion of binary numbers, George Boole (after which Boolean Algebra is known as) went about formalizing how computations could be carried out utilizing simply 0s and 1s. Consider this because the “discovery” of tips on how to do lengthy multiplication (for effectivity) after studying about repeated addition, permitting generalization and scalability of binary numbers.
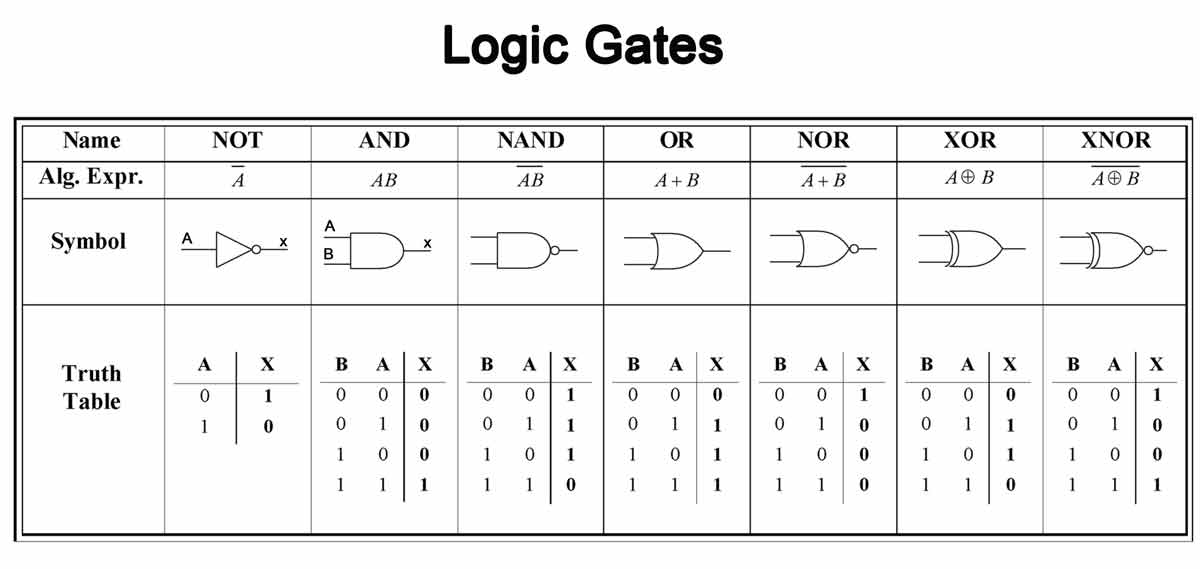
In 1847, Boole printed a paper known as, “The Mathematical Evaluation of Logic,” describing how an ON-OFF strategy can type the three most simple operations in digital logic: AND, OR, and NOT. With simply these three operations, Boolean operators enable for a basis to make use of binary to course of info. At the moment, we discover these three operators in all places inside our digital machines, primarily forming the Arithmetic Logical Unit (ALU) in modern day processors and plenty of directions of an Instruction Set Structure (ISA).
Whereas that is all nice, one of many basic limitations of binary numbers is how a lot info can they symbolize?
Let’s clarify this by instance: if we’ve got a single bit, representing 0 or 1, we will encode a complete of two various things. That’s, we will map the worth of “0” to symbolize a singular object, and map the worth of “1” for an additional object. Growing the variety of bits to 2, and we now have a mix of 00, 01, 10, and 11, or a complete of two^2 = 4 issues that may be represented.
This sample continues exponentially: if in case you have 8 bits (or a byte), you may symbolize as much as 2^8 = 256 distinctive issues. And naturally, with 32 bits, you may symbolize as much as 4,294,967,296 distinctive issues.
What are these “issues”? Effectively, within the area of numerics, it means you may “solely” symbolize somewhat above 4 billion distinctive numbers with 32 bits. This limitation turns right into a {hardware} downside, since numbers are basically limitless and infinite.
Thus, how do you go about representing an infinite set of numbers (together with integers, fractions, negatives, and maybe “particular” numbers like infinity) effectively in {hardware}? Herein lies the elemental concept behind {hardware} quantity representations.
The “Downside” with Numbers: 1970-1985
Numbers are infinite in nature. Mathematically talking, which means that it’s inconceivable to symbolize in {hardware} each single quantity from the most important exponents to the smallest decimals. Thus, a necessary query a processor designer must grapple with is, “Which numbers can/ought to the {hardware} assist?”
From an info principle perspective, the intently associated query of, “How many numbers could be represented?” is tied to the variety of bits accessible. This can be a sensible query that may be answered by the designer, particularly through the early microprocessor days when sources have been at a premium.
Going again to our instance above: suppose you select to symbolize numbers utilizing 8 bits. Meaning you may symbolize as much as 2^8 distinctive numbers, or 256 numbers. Which two-hundred and fifty-six quantity you select to symbolize is a special query.
- Do you assist simply the constructive integers, 0 to 255?
- Do you assist each constructive and detrimental integers centered round zero: -128 to +127.
- Or do you care about decimal numbers? As an example, you may select to assist 256 fractional values uniformly between 0 and 1: (0/256, 1/256, 2/256, … , 255/256).
Moreover, what do you do with the top factors? Within the final instance, do you select to symbolize 0 or 1? You do not have sufficient bits to symbolize each! With 8-bits, you may symbolize as much as 256 distinctive values from 0000 0000 to 1111 1111. For those who begin mapping them at 0 (for 0000 0000), then you may solely go as much as 255/256 = 0.99609375, and you haven’t any spare representations for the worth “1”!
One other problem is how do you deal with “bizarre” conditions, comparable to division by zero? Within the {hardware}, would you like that to be represented as “infinity”? Or perhaps reserve a bit illustration for “Not-a-Quantity (NaN)”? Which distinctive bit sequence do you put aside for these “denormals”?
Welcome to the world of digital illustration of numbers, the place you’re given a set price range of bits (e.g., 8, 16, or 32) and are tasked with encoding numbers effectively. To complicate issues additional, in a common goal processor you haven’t any concept what software might be operating on this {hardware}, and must deal with all exceptions and values gracefully. What do you do?
Within the Nineteen Seventies and early Nineteen Eighties, this led to the wild west of quantity codecs. Greater than 50 different number representations have been carried out in {hardware} designs, with varied design selections based mostly on the producers’ targets and desires.
This triggered an actual downside: two computer systems could be performing the identical mathematical operation (e.g., add, sub, mul, div), however produce completely different outcomes! This was particularly egregious in scientific computing functions, the place computational drift in values implies that small errors ultimately compounded to very large variations.
The IEEE-754 floating level customary was established in 1985 to deal with this. Particularly, code portability helped usher within the adoption of this customary. At the moment, so long as two computer systems are IEEE-754 compliant, then the identical mathematical operation is assured to end in the identical consequence. (We nonetheless have not addressed what that consequence can be — and what approximations IEEE-754 would make customary).

Since 1985, there have been two quantity format refreshes (in 2008 and 2019) which deal with some design bugs and introduce varied extensions for the usual. The main points of the refreshes are method too technical, however you may take a look at the Wikipedia article for specifics. Right here, we’ll simply give an summary of the design selections that have been made for the floating level customary, and why it’s known as a “floating” level.
IEEE-754 Floating Level Defined
The floating level customary was formally unveiled in 1985 by the IEEE, and was the brainchild of William Kahan. Kahan received the distinguished Turing Award (the computing equal for a Nobel Prize) just a few years later for his contributions because the “Father of Floating Level.” Accolades apart, what is Floating Level?
Not like the idea of a mounted decimal level, the Floating Level (FP) customary launched a scientific method of re-interpreting 32 bits by permitting the “level” between the entire a part of a quantity and the fractional a part of a quantity to alter. Analogously, it may be regarded as scientific notations, however with a constraint on which numbers are representable in {hardware}. The elemental tradeoff and distinction between a set level format and a floating level format is the vary and precision of the numbers being represented.
Let’s stroll via this.
Mounted Level Illustration
Recall from the knowledge principle primer above that with 32 bits, we will symbolize precisely 2^32 = 4,294,967,296 distinctive numbers. A set-point format, which is the normal method of encoding numbers in binary as envisioned by Leibniz, can symbolize solely a sure set of values relying on the place the decimal place is pegged.
For instance, let’s assume we allocate 1 signal bit, 15 integer bits, and 16 fractional bits (shorthand as (1, 15, 16) ) as follows:
With this illustration, the most important quantity we will encode is 32767.99998474121, and the smallest quantity we will encode is -32768. Moreover, there are particular numbers inside this vary that aren’t representable. For instance, if we wish to encode 21845.33333333, we discover that 32 bits doesn’t enable for that. If we needed to make use of this quantity on a machine with a set level (1, 15, 16) scheme, we must spherical it to one thing — for instance, the fractional half can be represented with .3333282470703125 because the closest “authorized” worth. And through the Wild West of quantity codecs, it actually was as much as the {hardware} designer to determine how and when to spherical.
One resolution is that we will transfer the decimal level and alter our implementation, maybe to a (1, 7, 24), or 1 signal bit, 7 integer bits, and 24 fractional bits. However that creates a brand new downside: by rising our precision, we needed to cut back the vary of numbers that may be represented. With a (1, 7, 24) allocation of bits, our vary now solely goes from 127.99999994039536 to -128. The worth of 21845 will not be even near being represented!
This was basically the issue with utilizing mounted level numerical representations, and earlier than the 1985 customary, each {hardware} vendor would principally select no matter vary and precision they deemed helpful for his or her functions. Throw within the problem of rounding, too, and we could be sure that not all 32-bit implementations of numbers are the identical.
Floating Level Illustration
Quite than sticking to a fundamental binary illustration, the Floating Level customary selected an alternate {hardware} information construction to get round this problem. As an alternative of allocating 32 bits into integer and fraction elements (which is intuitive to people), the FP customary makes use of an exponent and mantissa area for encoding numbers.
To drag this off, extra {hardware} is required to reinterpret the 32 bits, as proven under. One bit is reserved for the signal (+1 or -1), 8 bits are allotted for the exponent, and 23 bits are used for the mantissa. Then, you may merely plug the values into the next formulation (the place the bias is ready to 127), and get a worth from the 32-bits of 0s and 1s.
The thought is that you could now symbolize numbers throughout giant and small orders of magnitude through the exponent, after which have sufficient bits (the mantissa) for prime decision at these explicit magnitudes. The floating level (to generalize past the decimal or binary level) would modify to the magnitude of sure numbers utilizing exponentiation, and the mantissa can focus in on the specified quantity in that area.
Recall the dialogue about precision versus vary? Right here is the place it exhibits up: within the IEEE-754 customary, numbers close to zero have far more precision than numbers additional away from zero. That stated, you may nonetheless symbolize very giant and really small numbers (i.e., a big vary) since you have got 2^8 or 256 completely different representable exponent values (effectively, not precisely 256, however we’re coming to that).
An IEEE-754 Floating Level Instance
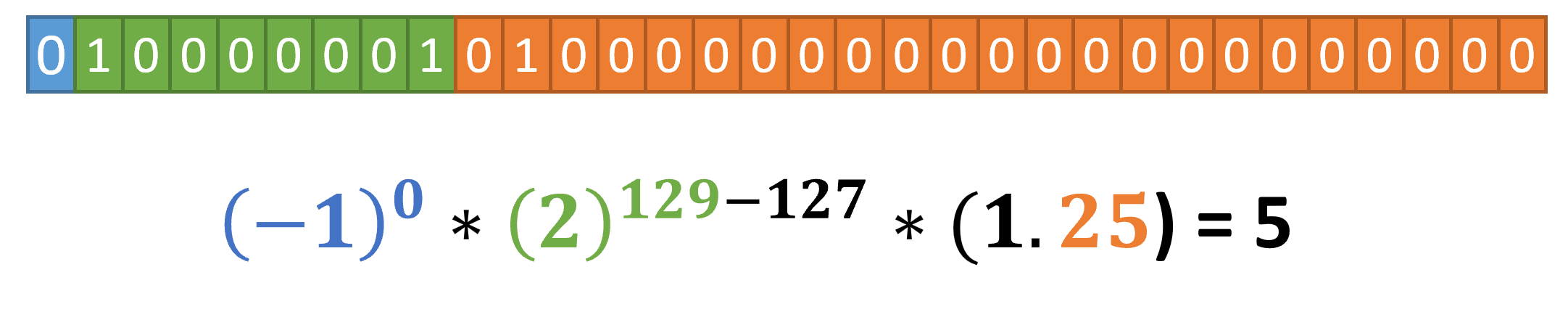
Let’s put this all collectively! How would we symbolize 5 in IEEE-754?
The signal bit is 0, since this can be a constructive quantity. For the exponent area, we have to get to the closest energy of two, which is 4, or 2^(2). Since there may be an implicit bias of 127 within the formulation, we’d like our exponent to be 129, or 10000001. With that, 129 – 127 = 2.
Lastly, we’d like 2^(2) x mantissa to equal 5, so the mantissa must encode 5/4 or 1.25. The 1 is implied, leaving us with 010 0000 0000 0000 0000 0000. Our closing 32 bit illustration is 0100 0000 1010 0000 0000 0000 0000 0000.
That is it!
Okay, effectively, that wasn’t as easy as somebody would assume. However, like Leibniz prompt greater than 400 years in the past, that is fairly simple for a pc to do, and now we will symbolize far more numbers with 32 bits than beforehand potential with a fixed-point scheme.
To avoid wasting you a while, here’s a handy calculator to mess around with floating level numbers.
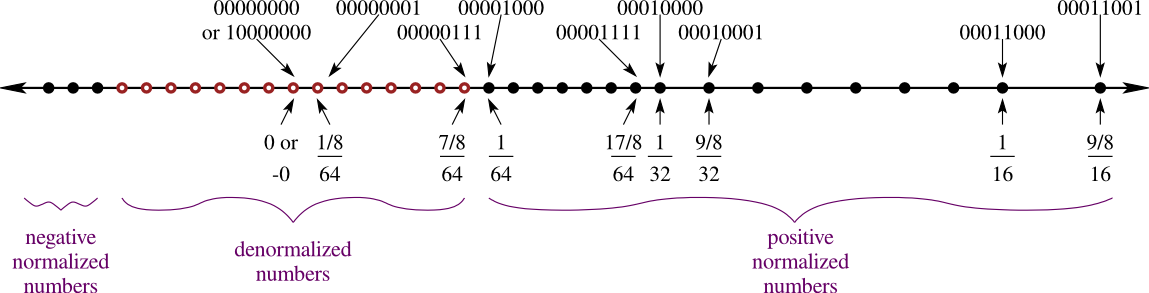
Particular values in IEEE-754 Floating Level
Though the exponent technically permits as much as 2^8 or 256 completely different representations, there are a few particular numbers reserved for “different” numbers. Particularly, if all of the bits are set to 1 (e.g., 1111 1111), then this particular quantity represents infinity if all of the mantissa bits are set to 0. If the mantissa bits are something apart from zero, then the bit illustration encodes “NaN”, or “Not a Quantity”. That is generally used as a method for signaling sure errors in {hardware}, the place sudden computations (comparable to divide-by-zero) could be recognized when an infinity or NaN pop up.
Equally, if all values are 0 (e.g., 0000 0000), then the mantissa bits are interpreted as subnormal numbers. In most floating-point quantity representations, regular numbers are represented with a non-zero mantissa and an exponent that falls inside a selected vary. In distinction, subnormal numbers have a mantissa that isn’t normalized, that means that the main little bit of the mantissa is zero, and the exponent is ready to the minimal representable worth. This permits subnormal numbers to symbolize very small values with restricted precision.
IEEE-754 Floating Level Customary takes maintain: 1985-2012
Following the introduction of the usual, the computing business nearly universally adopted IEEE-754 because the quantity format illustration for {hardware}. No main modifications or newsworthy designs occurred throughout these years.
In all probability probably the most notable number-format associated information merchandise was the 1994 Intel floating point division bug, which price the corporate almost half-a-billion {dollars} to deal with. This was an implementation problem within the Pentium processor. Though Intel claimed IEEE-754 compliance, a defective design led to computational error within the division operation, which (as talked about earlier) triggered computational drift points.
In addition to that, many jokes and memes amongst laptop science practitioners arose throughout this time. Regardless of being a typical, it was/continues to be troublesome to understand {that a} mathematical operation can have completely different outcomes than what a human would count on, but the {hardware} can nonetheless be completely compliant beneath the usual (!).
Nonetheless, within the final decade, the standardization of quantity codecs hit a highway bump. The rise of deep studying as a resurgent software area led to the rethinking of how numbers ought to be represented in {hardware}.
Deep Studying and Quantity Codecs: 2012 – Current
Few folks dabbled with the IEEE-754 customary for almost 30 years. And why would they: it had solved one of many largest issues with early computing: portability. That’s, any processor that was IEEE-754 compliant and carried out appropriately ought to have the identical numerical outcomes from one laptop to the following. This allowed for simpler packaging of functions and maintained a semblance of consistency in machines worldwide.
That modified roughly across the 12 months 2012, when deep neural networks (DNNs) took the world by a storm. Specifically, a graduate scholar on the College of Toronto named Alex Krizhevsky used his gaming Nvidia GPU to speed up neural community coaching, and received the ImageNet picture classification problem. Since then, companies have been scrambling to undertake synthetic intelligence in a myriad of functions, and {hardware} corporations specifically have been occupied with maximizing the efficiency of DNNs.
Specifically, corporations comparable to Nvidia, AMD, Intel, and Google started rethinking how numbers ought to be represented in {hardware}. The perception being that if there may be details about the appliance operating on the {hardware}, you may optimize the {hardware} considerably relatively than counting on common goal processors. And one explicit {hardware} optimization is altering the precision and vary of numbers for DNNs.
Because it seems, DNNs do not want a full 32 bits to symbolize the standard values noticed throughout coaching or inference. Additional, rounding was sometimes acceptable to some extent (so long as values did not collapse to zero throughout DNN coaching). A logical optimization then is to scale back the variety of exponent bits and mantissa bits. Fortunately, there already exists such an optimization within the IEEE-754 customary, known as Half Float.
A Half Float is strictly that: 16 bits as a substitute of 32 bits. Additional, the allocation of exponent and mantissa can be decreased: the exponent bits go down to five and the mantissa bits go all the way down to 10.
This easy optimization can sometimes double your efficiency, since now fewer bits are required for computation, and few bits must be shuffled round to and from reminiscence.
From an software perspective although, fewer bits did cut back the DNN accuracy. For sure software domains which are safety-critical, comparable to self-driving automobiles, that accuracy discount may not be well worth the higher efficiency. What else could possibly be accomplished?
Effectively, who stated the 16 bits wanted to observe the IEEE-754 customary in a (1, 5, 10) format? And that is the place corporations started taking cost and reimplementing quantity codecs, in an try and steadiness efficiency versus accuracy.
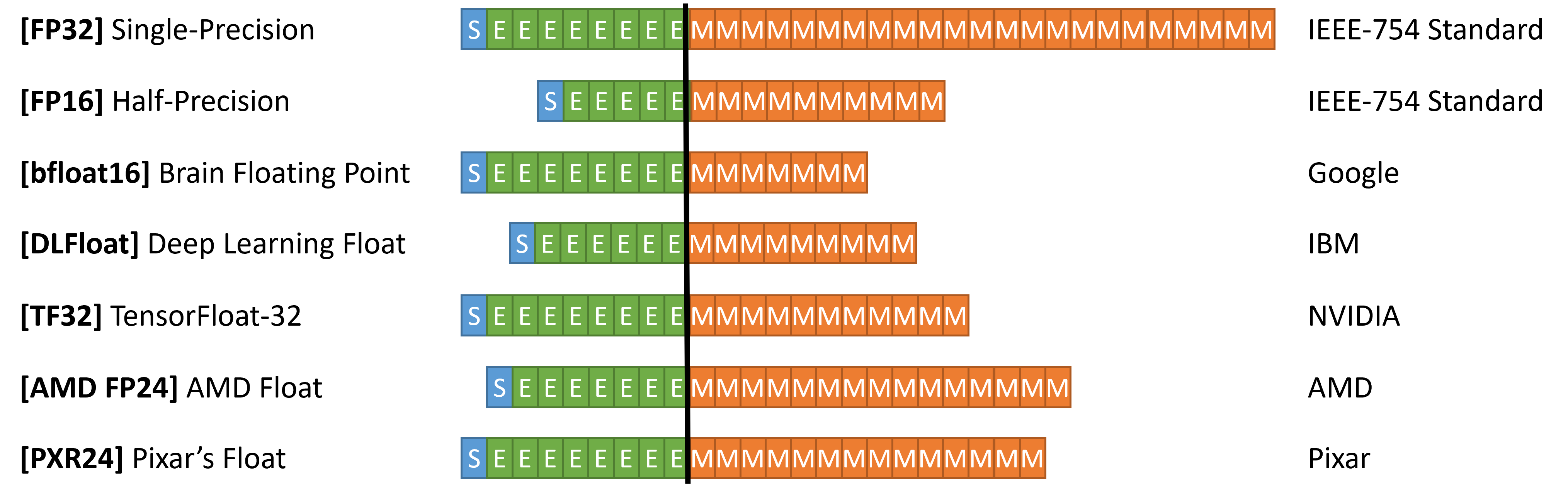
Floating Level Variants
Google was first. They went with a (1, 8, 7) format, placing forth extra bits in direction of the exponent (influencing the vary of numbers representable) on the expense of numerical precision. Taking a look at it from one other angle, this format mimicks the vary of full FP32, however cuts down on mantissa bits, which could possibly be thought-about pointless for this software. Popping out of Google Mind, they aptly named this new format Mind Float, or BFloat for brief.
BFloat did extraordinarily effectively, particularly throughout DNN coaching when values received very shut 0 and wanted to be represented. Different quantity codecs quickly adopted from different corporations, together with IBM, Nvidia, and AMD.
IBM’s 16-bit format, known as DeepFloat, allocates 6 bits for exponent and 9 bits for the mantissa (1, 6, 9). Nvidia went with an fascinating 20-bit format known as TensorFloat32 (as a result of it purported getting FP32 accuracy with simply 20-bits), assigning 8 exponent bits and 11 mantissa bits (1, 8, 11). AMD went up a bit extra, creating AMD FP24, a format with 7 exponent bits and 16 bits for the mantissa.
Essentially although, all these codecs didn’t diverge an excessive amount of from the IEEE-754 customary, by way of how the values have been interpreted. What modified was how the vary and precision of the numbers have been reachable, as a perform of the variety of exponent and mantissa bits.
In a current try and “standardize” quantity codecs throughout corporations, Nvidia, Arm, and Intel got here up with a new standard for FP8, an 8-bit quantity format. FP8 is a little more fascinating than the beforehand talked about codecs, as a result of it’s really 2 quantity codecs under-the-hood: a (1,5,2) configuration and a (1,4,3) configuration. The thought is that to adjust to this customary, the {hardware} ought to be capable of change between and permit each quantity codecs to work, with portability in thoughts.
Block Float
Why cease at simply altering the that means of numbers in {hardware}? What if you can also make just a few {hardware} modifications to make issues run even sooner?
That is the trail Microsoft took with Block Float. The instinct behind Block Float is that in lots of DNN functions, many values even have the identical exponent worth, however differ of their mantissa values. Stated in a different way, the values do not span a wide variety. Thus, why not extract the exponent bits and share them throughout a bunch of values, and solely retailer the mantissa bits?
The determine above illustrates how block float works. Relying on how giant a block is (say 8, 16, 32 values), you will get some vital financial savings in storage and communication bandwidth, by shuffling fewer bits round. It does take a little bit of smarts to determine the suitable granularity for exponent sharing, and also you would possibly want a devoted register (or a pair) in {hardware} to assist a number of simultaneous blocks, however the efficiency advantages communicate for themselves.
Surprisingly, the idea of Block Float really got here up within the Nineteen Seventies, through the Wild West of quantity codecs. Its resurgence as we speak largely has to do with the domain-specific {hardware} optimizations, concentrating on AI. By understanding somewhat one thing concerning the operating program (i.e., that values sometimes function in the identical vary of values), you may carry out hardware-centric optimizations to get efficiency speed-ups.
AdaptivFloat
One other cool quantity format that not too long ago emerged is named AdaptivFloat. This quantity format got here from a Harvard research lab in 2020, and independently adopted by Tesla for his or her Dojo structure, known as CFloat.
The fundamental concept behind AdaptivFloat is to introduce a quantity format that may dynamically adapt to the values in every layer of a DNN. Values inside a layer sometimes don’t span a variety themselves, however throughout layers they might differ. Thus, adapting the numerical illustration in {hardware} to the software program values effectively would give one of the best of each worlds in efficiency (through shorter bitwidths) and accuracy (by being extra trustworthy to numerical precision).
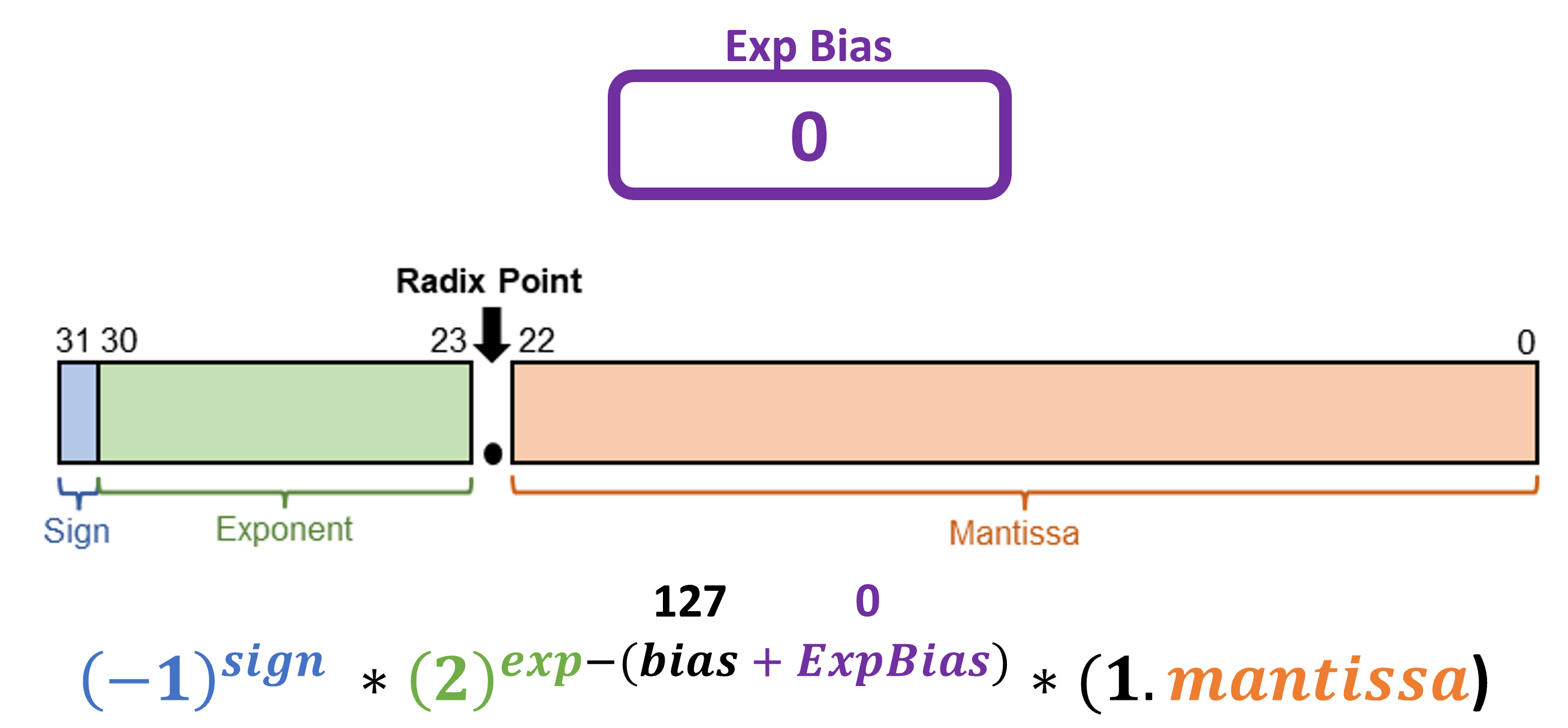
How does AdaptivFloat accomplish that? By adaptively altering the exponent bias within the floating level customary. Recall that within the IEEE-754 format, there may be an implicit bias of 127 utilized to exponent values. This comes up within the formulation as effectively, the place the exponent worth represented in binary must be subtracted by 127, after which this worth is used for the exponent.
What occurs for those who change the implicit 127 to one thing like 125? You primarily transfer the floating level to a different vary of values, for the reason that exponent modified (within the determine above, ExpBias can be -2). Intuitively, AdaptivFloat manipulates the dynamic vary of values on the layer granularity, utilizing minimal {hardware} overhead to alter the exponent bias. Thus, by including a easy register to offset and adapt to the numbers you wish to categorical, you may more-or-less maintain a variety of the identical {hardware}, however mess around with the dynamic vary.
AdaptivFloat is a intelligent little {hardware} trick that’s positively application-inspired. By unpacking the IEEE-754 customary and altering fundamental assumptions (on this case, the implicit exponent bias), AdaptivFloat exhibits each good accuracy and efficiency in comparison with Block Float and different quantity codecs, as explored within the analysis paper. Additional, it may be mixed with different bit allocations (as in, what number of exponent and mantissa bits ought to be used?), leading to varied variations comparable to CFloat16 and CFloat8, as employed by Tesla.
Posits and Unum
The ultimate quantity format we current are posits. Posits are literally not DNN-inspired, and the idea has been in growth for a handful of years as a floating point alternative. Their fundamental benefit is that they’ll squeeze out a fair bigger dynamic vary in comparison with floating level, for a given bitwidth.
One of many key options of the posit format is its use of a “variable-length exponent” which permits for extra environment friendly illustration of small numbers and a wider dynamic vary in comparison with fixed-point codecs. Moreover, the posit format has a well-defined and rigorous mathematical basis, making it well-suited to be used in scientific and engineering functions.
In comparison with the normal FP32 customary, posits have an additional area for the regime. The regime bits are used to find out the magnitude of a quantity and to differentiate between completely different ranges of values.
Within the posit format, the regime bits are used to specify the placement of probably the most vital non-zero little bit of the quantity, which determines the magnitude of the quantity. The variety of regime bits used can range relying on the particular implementation, however sometimes ranges from 1 to three bits. The worth of the regime bits determines the vary of the quantity and the place of the exponent area within the total encoding.
The regime bits are an essential a part of the posit format, as they permit for extra environment friendly illustration of small numbers and a wider dynamic vary in comparison with conventional fixed-point codecs. In addition they play an important function within the accuracy and efficiency of arithmetic operations carried out within the posit format.
Posits present immense potential, particularly in scientific computing functions. They’ve but to completely take off in {hardware} although, largely as a result of one thing seismic would wish to occur to persuade distributors to maneuver away from the IEEE customary. However, it presents a substitute for floating level, and plenty of {hardware} corporations are conserving it of their radar.
Future Implications
Who would have thought that quantity representations in {hardware} could possibly be so various and be revisited by main gamers in business lately? The AI revolution certainly deserves a variety of credit score for this current shift, but additionally the diminishing returns of Moore’s regulation and Dennard’s scaling which require extra architectural ingenuity to squeeze out extra efficiency out of the {hardware}.
Past runtime efficiency and DNN accuracy enhancements, one other essential consideration that has not too long ago come up is the reliability of latest quantity codecs within the context of single-bit upsets. Google and Meta have not too long ago made calls to motion from {hardware} corporations to look into random failures of their datacenters, originating from manufacturing and transient bit flips. With so many new quantity codecs being launched, it does name into query which bits are probably the most susceptible, and whether or not sure quantity codecs (comparable to AdaptivFloat) are more robust to the influence of bit flips due to their implementation.
The influence on code portability may also be fascinating to observe. The entire level of IEEE-754 was to formalize and standardize what to anticipate when a bit of code was run on completely different {hardware} gadgets. With AI, the declare is that there exists some fuzziness in computations which could be exploited for efficiency beneficial properties, and thus the rise of many reinterpretations of the usual. How will this influence future processor and accelerator design?
However in addition to the current design traits for numerical quantity representations in {hardware}, it’s nonetheless a marvel to see how a lot issues have modified since Leibniz’s fascination with a “quick” technique to do math. And will probably be thrilling to see the place issues take us within the subsequent 10-15 years on this enviornment.
What’s in a quantity? Effectively, much more than what seems at face worth for certain.
Source link